在做解方程练习时,学习卷中有一个方程“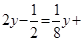 ■”中的■没印清晰,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当
■”中的■没印清晰,小聪问老师,老师只是说:“■是一个有理数,该方程的解与当 时代数式
时代数式 的值相同.”聪明的小聪很快补上了这个常数.同学们,请你们也来补一补这个常数.
的值相同.”聪明的小聪很快补上了这个常数.同学们,请你们也来补一补这个常数.
已知二次函数的图象的一部分如图所示,求:
(1)这个二次函数关系式,
(2)求图象与x轴的另一个交点,
(3)看图回答,当x取何值时y ﹤0.
如图,已知A、B是线段MN上的两点,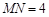 ,
, ,
, .以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设
.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设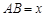 .
.
(1)求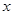 的取值范围;
的取值范围;
(2)若△ABC为直角三角形,求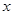 的值.
的值.
已知:如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP、BP、CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数.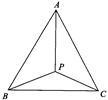
已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长. 
某商品进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品售价每上涨1元,则每个月少卖2件.设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?