“节能环保，低碳生活”是我们倡导的一种生活方式，某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台，三种家电的进价和售价如表所示：
| 价格种类 |
进价（元/台） |
售价（元/台） |
| 电视机 |
5000 |
5500 |
| 洗衣机 |
2000 |
2160 |
| 空调 |
2400 |
2700 |
（1）在不超出现有资金的前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案？
（2）在“2012年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在（1）的条件下，若三种电器在活动期间全部售出，商家预估最多送出多少张？
如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α.
（1）问题发现
① 当
时，
；② 当
时，
（2）拓展探究
试判断：当0°≤α＜360°时，
的大小有无变化？请仅就图2的情况给出证明.
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.
某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
① 金卡售价600元/张，每次凭卡不再收费；
② 银卡售价150元/张，每次凭卡另收10元.
暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数. 设游泳x次时，所需总费用为y元.
（1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
（2）在同一个坐标系中，若三种消费方式对应的函数图像如图所示，请求出点A、B、C的坐标；
（3）请根据函数图象，直接写出选择哪种消费方式更合算.
如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，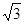
≈1.73）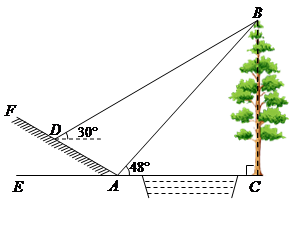
已知关于x的一元二次方程（x-3）（x-2）=|m|.
（1）求证：对于任意实数m，方程总有两个不相等的实数根；
（2）若方程的一个根是1，求m的值及方程的另一个根.
为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图.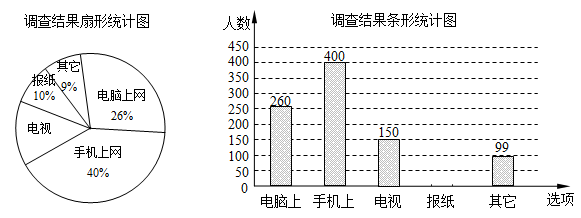
根据以上信息解答下列问题：
（1）这次接受调查的市民总人数是 ；
（2）扇形统计图中，“电视”所对应的圆心角的度数是 ；
（3）请补全条形统计图；
（4）若该市约有80万人，请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.