已知曲线C上动点P(x,y)到定点F1( ,0)与定直线l1∶x=
,0)与定直线l1∶x=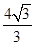 的距离之比为常数
的距离之比为常数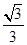 .
.
(1)求曲线C的轨迹方程;
(2)以曲线C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与曲线C交于点M与点N,求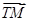 ·
· 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.
(本小题满分10分)
设△ABC的内角A、B、C所对的边分别为a,b,c,且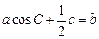 .
.
(1)求角A的大小;
(2)求 的取值范围。
的取值范围。
已知函数. ,直线/的方程为
,直线/的方程为
(1)若直线l是曲线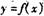
 .的切线,求证I
.的切线,求证I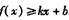 对任意
对任意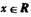 成立;
成立;
(2)若 对任意
对任意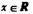 成立,求实数k,b应满足的条件.
成立,求实数k,b应满足的条件.
巳知抛物线y2 =4x,过点的M(0,2)直线l与抛物线交与A,B两点,且直线与X轴交于 点C
点C
(1)求证: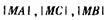 成等比数列;
成等比数列;
(2)设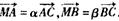 ,试问,
,试问,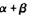 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.
如图,长方体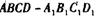 中,DA = DC
中,DA = DC =2,
=2,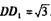 ’E是
’E是 的中点,F是C/:的中点.
的中点,F是C/:的中点.
(1)求证: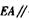 平面BDF
平面BDF
(2)求证:平面BDF 平面
平面
(3)求二面角D-EB-C的正切值.
工人在包装某产品肘不小心把两件不合格的产品一起放进了一个箱子里,此时该箱子中共有外观完全相同的六件产品,只有将产品遂-打开检查才能确定哪两件产品是不合格的,产品一旦打开检验不管是否合格都报废,记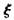 表示将两件不合格产品全部检测出来后四件合格产品中报废品的数量.
表示将两件不合格产品全部检测出来后四件合格产品中报废品的数量.
(1)求报废的合格品少于两件的概率;
(2)求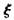 的分布列和数学期望.
的分布列和数学期望.