正四面体ABCD的体积为V,P是正四面体ABCD的内部的一个点.
(1)设“VPABC≥ V”的事件为X,求概率P(X);
V”的事件为X,求概率P(X);
(2)设“VPABC≥ V”且“VPBCD≥
V”且“VPBCD≥ V”的事件为Y,求概率P(Y).
V”的事件为Y,求概率P(Y).
已知椭圆C: +
+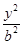 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
设椭圆 +
+ =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 ·
· +
+ ·
· =8,求k的值.
=8,求k的值.
已知椭圆C: +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P( ,
, ).
).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,2 ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
椭圆C: 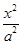 +
+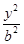 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=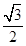 ,a+b=3.
,a+b=3.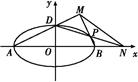
(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明2m-k为定值.
已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.