椭圆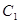 以双曲线
以双曲线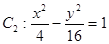 的实轴为短轴、虚轴为长轴,且与抛物线
的实轴为短轴、虚轴为长轴,且与抛物线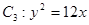 交于
交于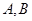 两点.
两点.
(1)求椭圆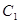 的方程及线段
的方程及线段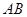 的长;
的长;
(2)在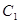 与
与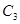 图像的公共区域内,是否存在一点
图像的公共区域内,是否存在一点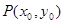 ,使得
,使得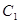 的弦
的弦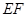 与
与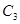 的弦
的弦 相互垂直平分于点
相互垂直平分于点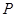 ?若存在,求点
?若存在,求点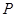 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图像如图所示,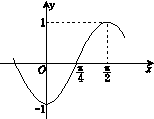
(1)求ω,φ的值;
(2)设g(x)=2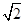 f
f f
f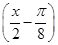 -1,当x∈[0,
-1,当x∈[0,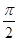 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
已知函数f(x)= .
.
(1)求函数f(x)的定义域;
(2)设α是第四象限的角,且tan α=- ,求f(α)的值.
,求f(α)的值.
在△ABC中,内角A,B,C所对的边分别为a,b,c,cos B=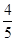 .
.
(1)求cos(A+C)的值;
(2)求sin 的值;
的值;
(3)若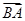 ·
·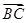 =20,求△ABC的面积.
=20,求△ABC的面积.
在△ABC中,内角A,B,C所对的边分别为a,b,c,且f(A)=2cos 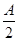 sin
sin +sin2
+sin2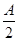 -cos2
-cos2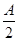 .
.
(1)求函数f(A)的最大值;
(2)若f(A)=0,C= ,a=
,a=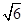 ,求b的值.
,求b的值.
已知函数f(x)=2 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间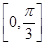 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若f(A)=1,sin B=3sin C,△ABC的面积为 ,求边长a.
,求边长a.