已知椭圆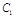 :
: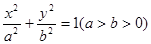 的离心率为
的离心率为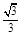 ,直线
,直线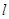 :
: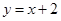 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆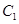 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆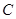 的方程;
的方程;
(2)过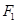 的直线
的直线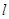 交椭圆
交椭圆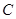 于
于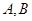 两点,则
两点,则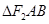 的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
(本小题满分12分)
已知函数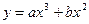 ,当
,当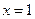 时,有极大值
时,有极大值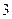 .
.
(1)求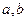 的值; (2)求函数
的值; (2)求函数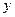 的极小值。
的极小值。
(1) 以直角坐标系的原点 为极点,
为极点, 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点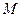 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,圆
,圆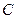 以
以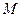 为圆心、
为圆心、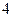 为半径。(I)求直线
为半径。(I)求直线 的参数方程和圆
的参数方程和圆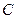 的极坐标方程;(II)试判定直线
的极坐标方程;(II)试判定直线 和圆
和圆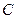 的位置关系.
的位置关系.
(2)把曲线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 轴的反射变换变为曲线
轴的反射变换变为曲线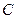 ,求曲线
,求曲线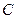 的方程.
的方程.
(3)关于 的一元二次方程
的一元二次方程 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围.
已知函数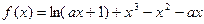 .(Ⅰ) 若
.(Ⅰ) 若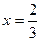 为
为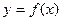 的极值点,求实数
的极值点,求实数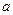 的值;(Ⅱ) 若
的值;(Ⅱ) 若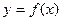 在
在 上为增函数,求实数
上为增函数,求实数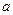 的取值范围;
的取值范围;
(Ⅲ) 若 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围。
的取值范围。
设椭圆 的离心率
的离心率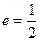 ,右焦点到直线
,右焦点到直线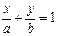 的距离
的距离
 为坐标原点。
为坐标原点。
(I)求椭圆 的方程;
的方程;
(II)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点,证明点
两点,证明点 到直
到直
线 的距离为定值,并求弦
的距离为定值,并求弦 长度的最小值
长度的最小值
为了迎接2009年10月1日建国60周年,某城市为举办的大型庆典活动准备了四种保证安全的方案,列表如下:
| 方案 |
A |
B |
C |
D |
| 经费 |
300万元 |
400万元 |
500万元 |
600万元 |
| 安全系数 |
0.6 |
0.7 |
0.8 |
0.9 |
其中安全系数表示实施此方案能保证安全的系数,每种方案相互独立,每种方案既可独立用,又可以与其它方案合用,合用时,至少有一种方案就能保证整个活动的安全。
(I)若总经费在1200万元内(含1200万元),如何组合实施方案可以使安全系数最高?
(II)要保证安全系数不小于0.99,至少需要多少经费?