某校高三年级文科学生600名,从参加期末考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
| 分组 |
频数 |
频率 |
| [45,60) |
2 |
0.04 |
| [60,75) |
4 |
0.08 |
| [75,90) |
8 |
0.16 |
| [90,105) |
11 |
0.22 |
| [105,120) |
15 |
0.30 |
| [120,135) |
a |
b |
| [135,150] |
4 |
0.08 |
| 合计 |
50 |
1 |
(1)写出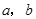 的值;
的值;
(2)估计该校文科生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在[135,150]中选两位同学,来帮助成绩在[45,60)中的某一位同学.已知甲同学的成绩为56分, 乙同学的成绩为145分,求甲乙在同一小组的概率.
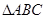 中,内角
中,内角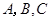 的对边分别是
的对边分别是 ,已知
,已知 成等比数列,且
成等比数列,且 .
.
(1)求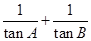 的值;
的值;
(2)设 ,求
,求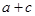 的值.
的值.
已知函数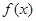 的定义域
的定义域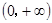 ,若
,若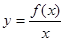 在
在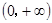 上为增函数,则称
上为增函数,则称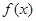 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在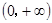 上为增函数,则称
上为增函数,则称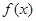 为“二阶比增函数”。把所有由“一阶比增函数”组成的集合记为
为“二阶比增函数”。把所有由“一阶比增函数”组成的集合记为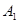 ,把所有由“二阶比增函数”组成的集合记为
,把所有由“二阶比增函数”组成的集合记为 .
.
(1)已知函数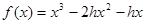 ,若
,若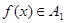 且
且 ,求实数
,求实数 的取值范围;
的取值范围;
(2)已知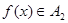 ,且存在常数
,且存在常数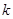 ,使得对任意的
,使得对任意的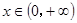 ,都有
,都有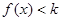 ,求
,求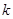 的最小值.
的最小值.
已知椭圆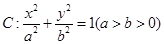 的离心率为
的离心率为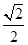 ,其左,右焦点分别为
,其左,右焦点分别为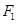 ,
, ,点
,点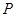 是坐标平面内一点,且
是坐标平面内一点,且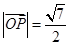 ,
,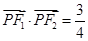 ,其中
,其中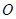 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)过点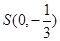 ,且斜率为
,且斜率为 的动直线
的动直线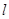 交椭圆于
交椭圆于 两点,在
两点,在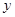 轴上是否存在定点
轴上是否存在定点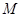 ,使以
,使以 为直径的圆恒过这个定点?若存在,求出点
为直径的圆恒过这个定点?若存在,求出点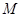 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
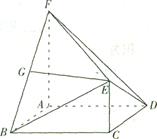
如图,在多面体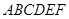 中,
中,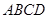 为菱形,
为菱形,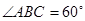 ,
,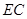
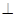 平面
平面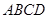 ,
,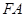
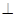 平面
平面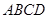 ,
,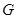 为
为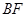 的中点,若
的中点,若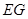
 平面
平面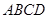 .
.
(1)求证: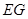
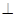 平面
平面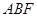 ;
;
(2)若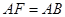 ,求二面角
,求二面角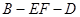 的余弦值.
的余弦值.