已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象;若
的图象;若 在
在 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.
已知数列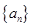 满足:
满足: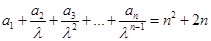 (其中常数
(其中常数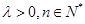 ).
).
(1)求数列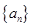 的通项公式;
的通项公式;
(2)当 时,数列
时,数列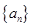 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
在平面 内,不等式
内,不等式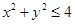 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组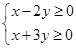 确定的平面区域为
确定的平面区域为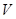 .
.
(1)定义横、纵坐标为整数的点为“整点”. 在区域 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域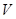 中的概率;
中的概率;
(2)在区域 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域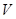 中的个数为
中的个数为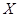 ,求
,求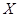 的分布列和数学期望.
的分布列和数学期望.
如图,在梯形△ABCD中,AB//CD,AD=DC-=CB=1, ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.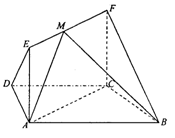
(1)求证:BC⊥平面ACFE;
(2)若M为线段EF的中点,设平面MAB与平面FCB所成角为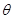 ,求
,求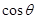 .
.
在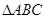 中,
中,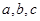 分别是角
分别是角 的对边,
的对边,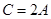 ,
, .
.
(1)求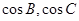 的值;
的值;
(2)若 ,求边
,求边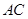 的长.
的长.
设数列 的前
的前 项和为
项和为 ,满足
,满足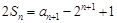 ,
,
 ,且
,且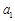 ,
,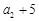 ,
,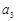 成等差数列.
成等差数列.
(1)求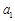 ,
, 的值;
的值;
(2) 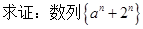 是等比数列
是等比数列
(3)证明:对一切正整数 ,有
,有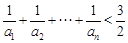 .
.