如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证: EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
已知数列{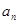 }中,
}中,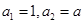 ,且
,且 对任意正整数都成立,数列{
对任意正整数都成立,数列{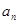 }的前n项和为Sn。
}的前n项和为Sn。
(1)若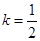 ,且
,且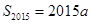 ,求a;
,求a;
(2)是否存在实数k,使数列{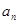 }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项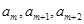 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若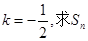 。
。
如图,某商业中心O有通往正东方向和北偏东30º方向的两条街道,某公园P位于商业中心北偏东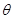 角(
角(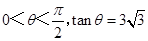 ),且与商业中心O的距离为
),且与商业中心O的距离为 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。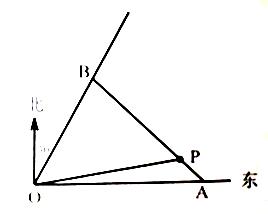
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
在三棱锥P-ABC中,D为AB的中点。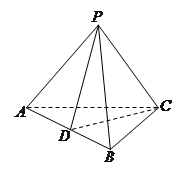
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC。
已知函数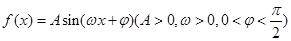 部分图象如图所示。
部分图象如图所示。
(1)求函数 的解析式;
的解析式;
(2)当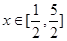 时,求函数
时,求函数 的值域。
的值域。
对于给定的大于1的正整数n,设 ,其中
,其中 ,且
,且 记满足条件的所有x的和为
记满足条件的所有x的和为 ,
,
(1)求 (2)设
(2)设 ,求
,求