如图;已知椭圆C: 的离心率为
的离心率为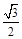 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: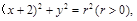 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.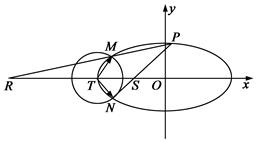
(1)求椭圆C的方程;
(2)求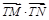 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与 轴交于点R,S,O为坐标原点。求证:
轴交于点R,S,O为坐标原点。求证: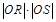 为定值.
为定值.
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系 中,圆锥曲线
中,圆锥曲线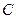 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
,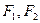 是圆锥曲线
是圆锥曲线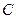 的左,右焦点.
的左,右焦点.
(Ⅰ)以原点为极点、 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(Ⅱ)在(I)的条件下,设直线 与圆锥曲线
与圆锥曲线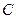 交于
交于 两点,求弦
两点,求弦 的长.
的长.
(本小题满分10分)选修4-1:几何证明选讲
如图,直线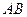 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且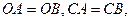 ⊙
⊙ 交直线
交直线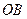 于
于 ,
,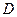 ,连接
,连接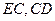 .
.
(Ⅰ)求证:直线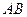 是⊙
是⊙ 的切线;
的切线;
(Ⅱ)若 ⊙
⊙ 的半径为
的半径为 ,求
,求 的长.
的长.
(本小题满分12分)
已知函数 (
( ,
, ),
), .
.
(Ⅰ)证明:当 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数 、
、 ,均有
,均有 成立;
成立;
(Ⅱ)记 ,
,
(ⅰ)若 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(ⅱ)证明: .
.
.(本小题满分12分)
已知椭圆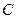 :
: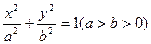 ,
, 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为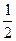 ,点
,点 在椭圆
在椭圆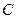 上,
上,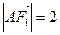 ,
,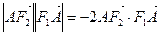 ,过
,过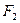 与坐标轴不垂直的直线
与坐标轴不垂直的直线 交椭圆于
交椭圆于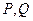 两点.
两点.
(Ⅰ)求椭圆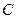 的方程;
的方程;
(Ⅱ)在线段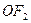 上是否存在点
上是否存在点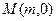 ,使得以线段
,使得以线段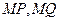 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数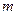 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题满分12分)
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村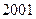 到
到 年十年间每年考入大学的人数.
年十年间每年考入大学的人数. 为方便计算,
为方便计算,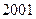 年编号为
年编号为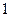 ,
, 年编号为
年编号为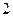 ,…,
,…, 年编号为
年编号为 .数据如下:
.数据如下:
(Ⅰ)从这 年中随机抽取两年,求考入大学人数至少有
年中随机抽取两年,求考入大学人数至少有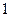 年多于
年多于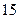 人的概率;
人的概率;
(Ⅱ)根据前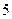 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出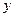 关于
关于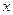 的回归方程
的回归方程 ,并计算第
,并计算第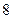 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.