已知抛物线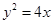 .
.
(1)若圆心在抛物线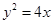 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线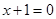 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线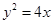 的焦点为
的焦点为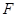 ,若过
,若过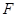 点的直线与抛物线相交于
点的直线与抛物线相交于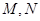 两点,若
两点,若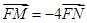 ,求直线
,求直线 的斜率;
的斜率;
(3)若过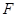 点且相互垂直的两条直线
点且相互垂直的两条直线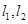 ,抛物线与
,抛物线与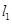 交于点
交于点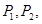 与
与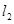 交于点
交于点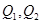 .
.
证明:无论如何取直线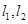 ,都有
,都有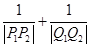 为一常数.
为一常数.
函数y=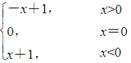 ,试写出给定自变量x,求函数值y的算法
,试写出给定自变量x,求函数值y的算法
写出解方程2x+7=0的一个算法.
已知一个等边三角形的周长为a,求这个三角形的面积.设计一个算法解决这个问题.
已知曲线C1: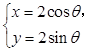 (
( 为参数),曲线C2:
为参数),曲线C2: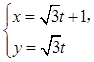 (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都拉伸为原来的两倍,分别得到曲线 .写出
.写出 的参数方程.
的参数方程.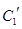 与
与 公共点的个数和C
公共点的个数和C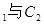 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
已知函数y=f(x)是定义在区间[-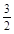 ,
,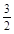 ]上的偶函数,且
]上的偶函数,且
x∈[0,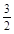 ]时,
]时,
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.