已知角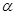 的终边经过点
的终边经过点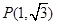 ,试写出角
,试写出角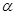 的集合M,并把集合M中在
的集合M,并把集合M中在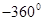 ~
~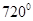 间的角写出来.
间的角写出来.
设数列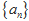 的前n项和为
的前n项和为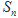 .已知
.已知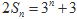 .
.
(I)求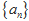 的通项公式;
的通项公式;
(II)若数列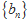 满足
满足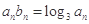 ,
, 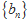 的前n项和
的前n项和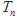 .
.
①求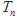 ;
;
②若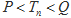 对于
对于 恒成立,求
恒成立,求 与
与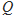 的范围.
的范围.
已知函数 .
.
(1)若当 时
时 在
在 上恒成立,求
上恒成立,求 范围;
范围;
(2)解不等式 .
.
如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C.景区管委会又开发了风景优美的景点D.经测量景点D位于景点A的北偏东30°方向上8 km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5 km.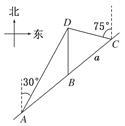
(1)景区管委会准备由景点D向景点B修建一条笔直的公路,不考虑其他因素,求出这条公路的长;
(2)求景点C和景点D之间的距离.参考数据:sin75°=
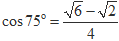
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
| 规格类型 钢板规格 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
2 |
1 |
1 |
| 第二种钢板 |
1 |
2 |
3 |
今需A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需A、B、C三种规格成品,且使所用的钢板的张数最少?