要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
| 规格类型 钢板规格 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
2 |
1 |
1 |
| 第二种钢板 |
1 |
2 |
3 |
今需A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需A、B、C三种规格成品,且使所用的钢板的张数最少?
已知数列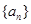 的前n项和
的前n项和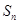 满足
满足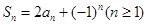
(1)写出数列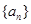 的前3项
的前3项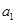 、
、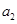 、
、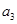 ;
;
(2)求数列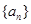 的通项公式;
的通项公式;
(3)证明对于任意的整数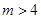 有
有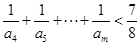
设函数
(1)画出 的简图;
的简图;
(2)若方程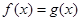 有三个不等实根,求k值的集合;
有三个不等实根,求k值的集合;
(3)如果 时,函数
时,函数 的图象总在直线
的图象总在直线 的下方,试求出k值的集合。
的下方,试求出k值的集合。
如果n件产品中任取一件样品是次品的概率为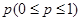 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
).
(1)求该企业日赢利额 的最大值;
的最大值;
(2)为保证每天的赢利额不少于日赢利额最大值的50%,试求该企业日产量的取值范围。
已知集合
(1)若 ,求实数m的值;
,求实数m的值;
(2)设全集为R,若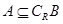 ,求实数m的取值范围。
,求实数m的取值范围。
等差数列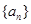 的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
(1)求此数列的公差d;
(2)当前n项和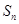 是正数时,求n的最大值。
是正数时,求n的最大值。