(本小题满分14分)如图,在四棱锥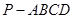 中,底面
中,底面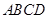 是正方形,
是正方形, 平面
平面 .点
.点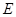 是线段
是线段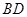 的中点,点
的中点,点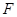 是线段
是线段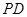 上的动点.
上的动点.
(Ⅰ)若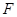 是
是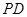 的中点,求证:
的中点,求证: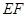 //平面
//平面 ;
;
(Ⅱ)求证: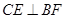 ;
;
(Ⅲ)若 ,
,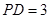 ,当三棱锥
,当三棱锥 的体积等于
的体积等于 时,试判断点
时,试判断点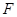 在边
在边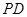 上的位置,并说明理由.
上的位置,并说明理由.
(本小题满分10分)宁波市的一家报刊点,从报社买进《宁波日报》的价格是每份0.20元,卖出的价格是每份0.3元,卖不掉的报纸可以以每份0.05元的价格退回报社。在一个月(30天计)里,有20天可以卖出400份,其余10天每天只能卖出250份,但是每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使得每月所获利润最大?并计算他一个月最多可以赚多少元?
(本小题满分10分)设函数
(1)证明函数是偶函数;
(2)若方程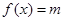 有两个根,试求
有两个根,试求 的取值范围。
的取值范围。
(本小题满分8分)
已知集合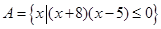 ,
, 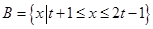 .若
.若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知定义域为 的单调函数
的单调函数 是奇函数,当
是奇函数,当 时,
时,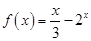 .
.
(I)求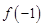 的值;
的值;
(II)求 的解析式;
的解析式;
(III)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数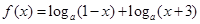 ,
,
(I)求函数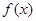 的定义域;
的定义域;
(II)若函数 ,求
,求 的值;
的值;
(III)若函数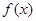 的最小值为
的最小值为 ,求
,求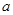 的值.
的值.