第16届亚运会于2010年11月12日在广州举办,运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务,且跳水场馆至少有一名广州大学志愿者的概率是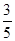 .
.
(1)求6名志愿者中来自广州大学、中山大学的各有几人?
(2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数,求X的分布列及均值.
将3个小球任意地放入4个玻璃杯中,杯子中球的最多个数为 ,求
,求 的分布列.
的分布列.
因冰雪灾害,某柑橘基地果林严重收损,为此有关专家提出一种拯救果树的方案,该方案需分两年实施且相互独立。该方案预计第一年可以使柑橘产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4;第二年可以使柑橘产量为第一年的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4,求两年后柑橘产量恰好达到灾前产量的概率.
(
已知三个函数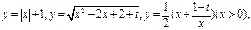 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的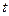 为同一个常数,且
为同一个常数,且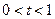 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程 的三个根.
的三个根.
(Ⅰ) 求证: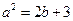 ;
;
(Ⅱ) 设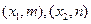 是函数
是函数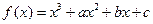 的两个极值点,求
的两个极值点,求 的取值范围.
的取值范围.
如图,已知直线 (
( )与抛物线
)与抛物线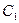 :
: 和圆
和圆 :
: 都相切,
都相切, 是
是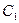 的焦点.
的焦点.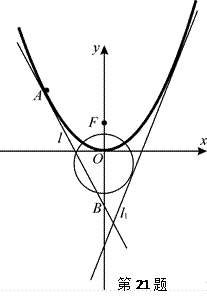
(Ⅰ)求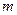 与
与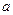 的值;
的值;
(Ⅱ)设 是
是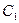 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线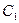 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点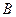 ,以
,以 、
、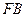 为邻边作平行四边形
为邻边作平行四边形 ,证明:点
,证明:点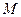 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点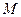 所在的定直线为
所在的定直线为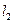 ,直线
,直线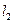 与
与 轴交点为
轴交点为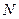 ,连接
,连接 交抛物线
交抛物线 于
于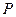 、
、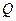 两点,求△
两点,求△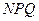 的面积
的面积 的取值范围.
的取值范围.
(
已知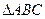 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面 平面
平面 ,过点
,过点 作
作 平面
平面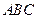 ,且
,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小.
所成角的大小.