若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
已知{an}是等差数列,a1=3,Sn是其前n项和,在各项均为正数的等比数列{bn}中,b1=1,且b2+S2=10,S5 =5b3+3a2.
(I )求数列{an}, {bn}的通项公式;
(II)设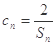 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证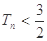
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响。已知甲回答这题正确的概率是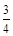 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是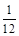 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是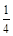 .
.
(I)求乙、丙两人各自回答这道题正确的概率;
(II)用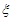 表示回答该题正确的人数,求
表示回答该题正确的人数,求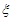 的分布列和数学期望
的分布列和数学期望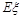 .
.
已知二次函数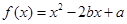 ,满足
,满足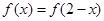 ,且方程
,且方程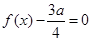 有两个相等的实根.
有两个相等的实根.
(1)求函数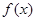 的解析式;
的解析式;
(2)当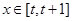
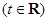 时,求函数
时,求函数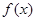 的最小值
的最小值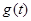 的表达式.
的表达式.
已知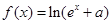 是定义域为R的奇函数,
是定义域为R的奇函数,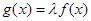 ,
,
⑴求实数 的值;
的值;
⑵若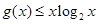 在x∈[2,3]上恒成立,求
在x∈[2,3]上恒成立,求 的取值范围.
的取值范围.
已知函数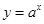
 在
在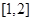 上的最大值与最小值之和为
上的最大值与最小值之和为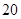 ,记
,记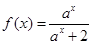 .
.
(1)求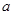 的值;
的值;
(2)证明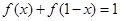 ;
;
(3)求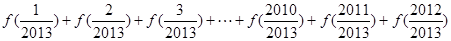 的值.
的值.