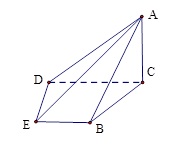
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD =" EF" = 1.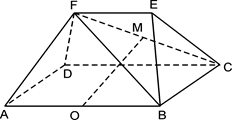
(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)
表示所取3张卡片上的数字的中位数,求
的分布列与数学期望.
(注:若三个数
满足
,则称
为这三个数的中位数).
已知函数
的图像关于直线
对称,且图像上相邻两个最高点的距离为 .
.
(1)求
和
的值;
(2)若
,求
的值.
已知函数 若 在 上的最大值和最小值分别记为 ,
(1)求
;
(2)设
若
对
恒成立,求
取值范围.
如图,设椭圆
,动直线
与椭圆
只有一个公共点
,且点
在第一象限.
(1)已知直线
的斜率为
,用
表示点
的坐标;
(2)若过原点
的直线
与
垂直,证明:点
到直线
的距离的最大值为
.
如图,在四棱锥 中,平面 , , , . .
(1)证明:
;
(2)求二面角
的大小