三角形ABC的三个顶点A(1,3)B(1,﹣3)C(3,3),求
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)三角形ABC的外接圆O1的方程;
(Ⅲ)已知圆O2: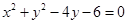 ,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。
,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。
如图,棱锥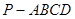 的底面
的底面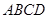 是矩形,
是矩形,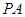 ⊥平面
⊥平面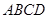 ,
, .
.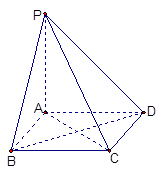
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B的大小;
(3)求点C到平面PBD的距离.
如图是一个正三棱柱(以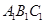 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为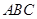 .已知
.已知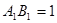 ,
,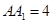 ,
,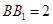 ,
,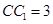 .
.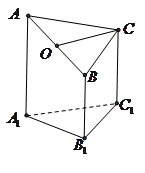
(1)设点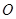 是
是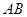 的中点,证明:
的中点,证明: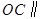 平面
平面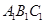 ;
;
(2)求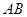 与平面
与平面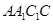 所成的角的正弦值;
所成的角的正弦值;
已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣9≤0},m∈R.
(1)若m=3,求A∩B;
(2)若A⊆B,求实数m的取值范围.
已知函数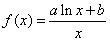 (其中
(其中 ),函数
),函数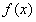 在点
在点 处的切线过点
处的切线过点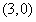 .
.
(Ⅰ)求函数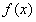 的单调区间;
的单调区间;
(Ⅱ)若函数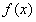 与函数
与函数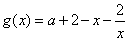 的图像在
的图像在 有且只有一个交点,求实数
有且只有一个交点,求实数 的取值范围.
的取值范围.