设椭圆
 的左、右焦点分别
的左、右焦点分别 、
、 ,点
,点 是椭圆短轴的一个端点,且焦距为6,
是椭圆短轴的一个端点,且焦距为6, 的周长为16.
的周长为16.
(I)求椭圆 的方程;
的方程;
(2)求过点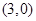 且斜率为
且斜率为 的直线
的直线 被椭圆
被椭圆 所截的线段的中点坐标.
所截的线段的中点坐标.
(本小题满分12分)已知函数f(x)=ax+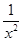 (x≠0,常数a∈R).
(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.
已知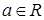 ,设命题
,设命题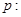 函数
函数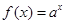 是
是 上的单调递减函数;命题
上的单调递减函数;命题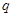 :函数
:函数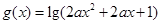 的定义域为
的定义域为 .若“
.若“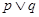 ”是真命题,“
”是真命题,“ ”是假命题,求实数
”是假命题,求实数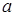 的取值范围.
的取值范围.
(满分12分)已知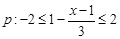 ,
,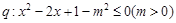 ,且
,且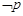 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数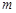 的取值范围.
的取值范围.
(本小题满分12分) 设函数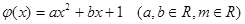
(1)若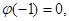 且对任意实数
且对任意实数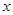 均有
均有 成立,求实数
成立,求实数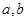 的值;
的值;
(2)在(1)的条件下,令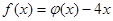 ,若
,若 与
与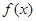 在
在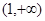 上有相同的单调性,
上有相同的单调性,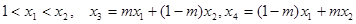 且
且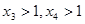 ,试比较
,试比较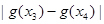 与
与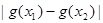 的大小
的大小
(本小题满分12分)已知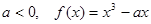
(1)判断 在
在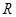 上的单调性,并证明.
上的单调性,并证明.
(2)设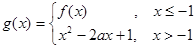 ,且
,且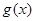 在
在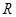 上是单调函数,求
上是单调函数,求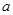 的取值范围.
的取值范围.