已知数列 的前n项和为
的前n项和为 ,且
,且
 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)令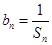 ,且数列
,且数列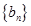 的前n项和为
的前n项和为 ,求
,求 ;
;
(3)若数列 满足条件:
满足条件: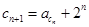 ,又
,又 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列 为等差数列?
为等差数列?
已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
已知数列{an}的前n项和Sn,求通项an.
(1)Sn=3n-1;
(2)Sn=n2+3n+1.
某学校拟建一块周长为400m的操场,如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?
某森林出现火灾,火势正以100m2/分钟的速度顺风蔓延,消防站接到报警立即派消防队员前去,在火灾发生后5分钟到达救火现场,已知消防队员在现场平均每人灭火50m2/分钟,所消耗的灭火材料,劳务津贴等费用为人均125元/分钟,另附加每次救火所耗损的车辆、器械和装备等费用人均100元,而烧毁森林的损失费60元/m2,应该派多少消防队员前去救火才能使总损失最少?
已知函数f(x)=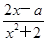 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设x1、x2是关于x的方程f(x)= 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.