设非空集合 满足:当
满足:当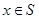 时,有
时,有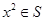 .给出如下命题:①若
.给出如下命题:①若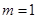 ,
,
则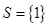 ;②若
;②若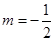 ,则
,则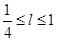 ;③若
;③若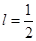 ,则
,则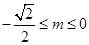 ;④若
;④若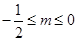 ,
,
则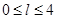 .其中所有正确命题的序号是.
.其中所有正确命题的序号是.
(本小题满分12分)
已知平行六面体中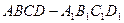 ,
,
各条棱长均为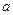 ,底面是正方形,且
,底面是正方形,且 ,
,
设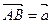 ,
, ,
,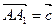 ,
,
(1)用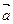 、
、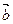 、
、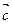 表示
表示 及求
及求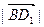 ;
;
(2)求异面直线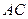 与
与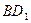 所成的角的余弦值。
所成的角的余弦值。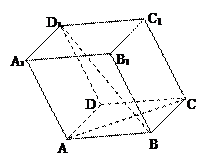
(本小题满分12分)
如图,棱锥P—ABCD的底面ABCD是矩形,
PA⊥平面ABCD,PA=AD=2, BD=
BD=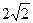 .
.
(1)求点C到平面PBD的距离.
|
(2)在线段 上是否存在一点
上是否存在一点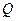 ,使
,使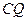 与平面
与平面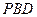 所成的角
所成的角
 ,若存在,指出点
,若存在,指出点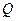 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

(本小题满分12 分)
如图 ,四棱锥
,四棱锥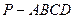 的底面是边长为
的底面是边长为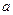 的菱形,
的菱形, ,
, 平面
平面 ,
, ,
,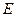 为
为 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
(1)求证:平面 平面
平面 ;
;
(2)求二面角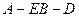 的正切值。
的正切值。
(本小题满分12 分)
已知正方体 ,
, 是底
是底 对角线的交点.
对角线的交点.
求证:(1) ∥面
∥面 ;
;
(2) 面
面 .
. 
已知α,β是平面 ,m,n是直线. 给出下列命题:
,m,n是直线. 给出下列命题:
①.若m∥n,m⊥α,则n⊥α②.若m⊥α,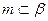 ,则α⊥β
,则α⊥β
③.若m⊥α,m⊥β,则α∥β④.若m∥α,α∩β=n,则m∥n其中,真命题的编号是_▲(写出所有正确结论的编号).