如下图,在四棱柱 中,底面
中,底面 和侧面
和侧面 都
都
是矩形,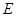 是
是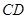 的中点,
的中点, ,
,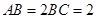 .
.
(1)求证: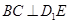
(2)求证: 平面
平面 ;
;
(3)若平面 与平面
与平面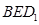 所成的锐二面角的大小为
所成的锐二面角的大小为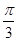 ,求线段
,求线段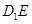 的长度.
的长度.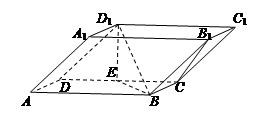

已ΔABC的内角A,B,C对的边分别为a,b,c =" (2a,C" -26) ,
=" (2a,C" -26) ,  = (cosC,l),且
= (cosC,l),且 丄
丄 .
.
(I)求角A的大小;
(II )若a = 1,求b +c的取值范围.
已知函数 .
.
(I)证明: ;
;
(II)求不等式 的解集.
的解集.
在直接坐标系 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数)
为参数)
(I)已知在极坐标(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4, ),判断点
),判断点 与直线
与直线 的位置关系;
的位置关系;
(II)设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
已知:如图, 为
为 的外接圆,直线
的外接圆,直线 为
为 的切线,切点为
的切线,切点为 ,直线
,直线 ∥
∥ ,交
,交 于
于 、交
、交 于
于 ,
, 为
为 上一点,且
上一点,且 .
.
求证:(Ⅰ) ;
;
(Ⅱ)点 、
、 、
、 、
、 共圆.
共圆.
已知函数 ,
, (
( ,
, 为常数,
为常数, ),且这两函数的图像有公共点,并在该公共点处的切线相同.
),且这两函数的图像有公共点,并在该公共点处的切线相同.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.