如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.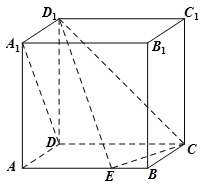
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45o,求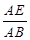 的值;
的值;
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。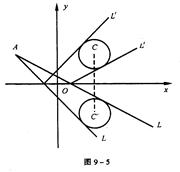
已知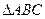 的顶点
的顶点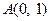 ,
,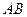 边上的中线
边上的中线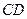 所在的直线方程为
所在的直线方程为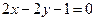 ,
,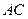 边上的高
边上的高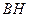 所在直线的方程为
所在直线的方程为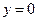 .
.
(1)求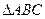 的顶点
的顶点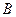 、
、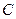 的坐标;
的坐标;
(2)若圆 经过不同的三点
经过不同的三点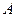 、
、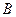 、
、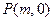 ,且斜率为
,且斜率为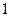 的直线与圆
的直线与圆 相切于点
相切于点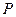 ,求圆
,求圆 的方程.
的方程.
设椭圆的中心在原点,焦点在x轴上,离心率e=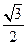 .已知点P
.已知点P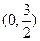 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为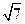 ,求这个椭圆的方程.
,求这个椭圆的方程.
已知圆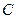 和
和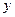 轴相切,圆心在直线
轴相切,圆心在直线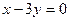 上,且被直线
上,且被直线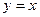 截得的弦长为
截得的弦长为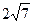
 ,求圆
,求圆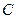 的方程。
的方程。
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为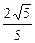 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线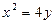 的焦点。
的焦点。
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若 的值。
的值。