已知椭圆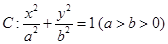 的离心率为
的离心率为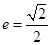 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的标准方程;
的标准方程;
(2)过右焦点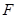 作斜率为
作斜率为 的直线
的直线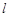 交曲线
交曲线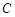 于
于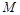 、
、 两点,且
两点,且 ,又点
,又点 关于原点
关于原点 的对称点为点
的对称点为点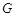 ,试问
,试问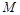 、
、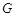 、
、 、
、 四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
经过点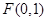 且与直线
且与直线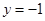 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为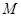 .点
.点 在轨迹
在轨迹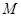 上,且关于
上,且关于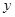 轴对称,过线段
轴对称,过线段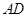 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线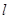 ,使直线
,使直线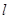 与轨迹
与轨迹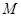 在点
在点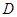 处的切线平行,设直线
处的切线平行,设直线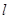 与轨迹
与轨迹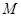 交于点
交于点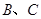 .
.
(1)求轨迹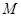 的方程;
的方程;
(2)证明: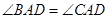 ;
;
(3)若点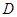 到直线
到直线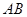 的距离等于
的距离等于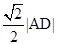 ,且
,且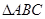 的面积为20,求直线
的面积为20,求直线 的方程.
的方程.
设函数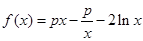 .
.
(1)若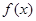 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数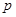 的取值范围;
的取值范围;
(2)设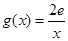 ,且
,且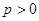 ,若在
,若在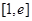 上至少存在一点
上至少存在一点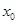 ,使得
,使得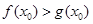 成立,求实数
成立,求实数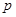 的取值范围.
的取值范围.
如图,在等腰梯形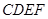 中,
中,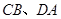 是梯形的高,
是梯形的高,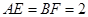 ,
,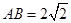 ,现将梯形沿
,现将梯形沿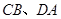 折起,使
折起,使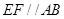 ,且
,且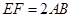 ,得一简单组合体
,得一简单组合体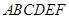 如图所示,已知
如图所示,已知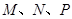 分别为
分别为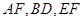 的中点.
的中点.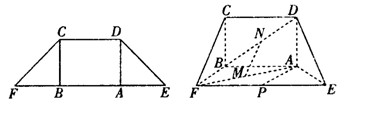
(1)求证: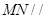 平面
平面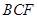 ;
;
(2)求证: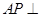 平面
平面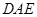 .
.
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成社团指导小组,有关数据见下表:(单位:人)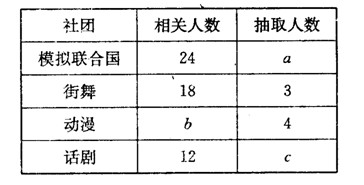
(1)求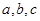 的值;
的值;
(2)若从“动漫”与“话剧”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
已知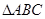 三个内角
三个内角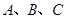 的对边分别为
的对边分别为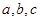 ,向量
,向量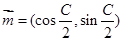 ,
,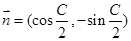 ,且
,且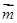 与
与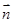 的夹角为
的夹角为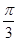 .
.
(1)求角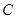 的值;
的值;
(2)已知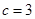 ,
,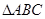 的面积
的面积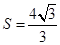 ,求
,求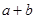 的值.
的值.