一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 (如图所示,其中O为圆心,
(如图所示,其中O为圆心, 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
二次函数
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y= f(x)的图像恒在y=2x+m的图像上方,试确定实数m的取值范围。
已知关于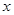 的不等式组
的不等式组 其中
其中
(1)求不等式(1)的解集;
(2)若不等式的解集为空集,求实数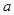 的取值范围。
的取值范围。
已知函数


 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的斜率为
处的切线的斜率为 ,问:
,问:  在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间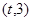 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间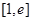 上至少存在一个
上至少存在一个 ,使得
,使得 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.
已知函数 ,
,
(Ⅰ)当 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
(Ⅱ)如果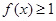 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围
如图,四棱锥 中,
中, ⊥底面
⊥底面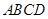 ,底面
,底面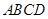 为梯形,
为梯形,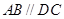 ,
,
 ,且
,且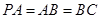 ,点
,点 是棱
是棱 上的动点.
上的动点.
(Ⅰ)当 ∥平面
∥平面 时,确定点
时,确定点 在棱
在棱 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的余弦值.
的余弦值.