在平面直角坐标系xOy中,设曲线C1: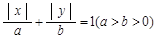 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线C1上的点到原点O的最短距离为
,曲线C1上的点到原点O的最短距离为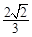 .以曲线C1与坐标轴的交点为顶点的椭圆记为C2.
.以曲线C1与坐标轴的交点为顶点的椭圆记为C2.
(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心O的任意弦,l是线段AB的垂直平分线.M是l上的点(与O不重合).
①若MO=2OA,当点A在椭圆C2上运动时,求点M的轨迹方程;
②若M是l与椭圆C2的交点,求△AMB的面积的最小值.
已知椭圆E: (
(


 0)过点(0,
0)过点(0, ),其左焦点
),其左焦点 与点P(1,
与点P(1, )的连线与圆
)的连线与圆 相切。
相切。
(1)求椭圆E的方程;
(2)设Q为椭圆E上的一个动点,试判断以 为直径的圆与圆
为直径的圆与圆 的位置关系,并证明
的位置关系,并证明
如图,P—ABCD是正四棱锥, 是正方体,其中
是正方体,其中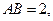

(1)求证: ;
;
(2)求平面PAD与平面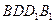 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(3)求 到平面PAD的距离
到平面PAD的距离
在△ABC中,a、b是方程x2-2mx+2=0的两根,且2cos(A+B)=-1
(1)求角C的度数;
(2)求△ABC的面积
已知函数 是增函数,
是增函数, 为减函数.
为减函数.
(1)求a的值;
(2)设函数 上的增函数,且对于
上的增函数,且对于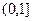 内的任意两个变量s、t,
内的任意两个变量s、t, 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)设 ,求证:
,求证: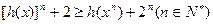
已知直线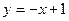 与椭圆
与椭圆 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量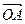 与向量
与向量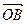 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率 时,求椭圆的长轴长的最大值
时,求椭圆的长轴长的最大值