我们将具有下列性质的所有函数组成集合M:函数 ,对任意
,对任意 均满足
均满足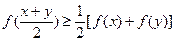 ,当且仅当
,当且仅当 时等号成立。
时等号成立。
(1)若定义在(0,+∞)上的函数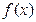 ∈M,试比较
∈M,试比较 与
与 大小.
大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
(本小题满分12分)已知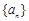 是正项数列,
是正项数列,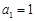 ,且点
,且点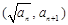 (
( )在函数
)在函数 的图像上.
的图像上.
(1)求数列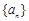 的通项公式;
的通项公式;
(2)若列数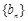 满足
满足 ,
,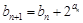 ,求证:
,求证: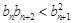 .
.
(本小题满分12分)已知椭圆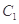 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为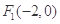 ,
,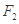
 ,点
,点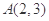 在椭圆
在椭圆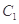 上,过点
上,过点 的直线
的直线 与抛物线
与抛物线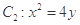 交于
交于 两点,抛物线
两点,抛物线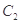 在点
在点 处的切线分别为
处的切线分别为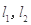 ,且
,且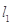 与
与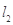 交于点
交于点 .
.
(Ⅰ)求椭圆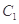 的方程;
的方程;
(Ⅱ)是否存在满足 的点
的点 ? 若存在,指出这样的点
? 若存在,指出这样的点 有几个(不必求出点
有几个(不必求出点 的坐标);若不存在,说明理由.
的坐标);若不存在,说明理由.
(本小题满分15分)已知二次函数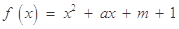 ,关于
,关于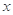 的不等式
的不等式 的解集为
的解集为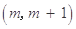 ,(
,( ),设
),设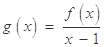 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数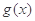 的一个极值点是
的一个极值点是 ,求
,求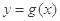 的值域;
的值域;
(Ⅲ)若函数 存在三个极值点,求
存在三个极值点,求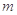 的取值范围.
的取值范围.
(本小题满分12分)如图,在正三棱柱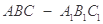 中,△
中,△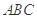 是边长为
是边长为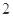 的等边三角形,
的等边三角形, 平面
平面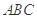 ,
, ,
, 分别是
分别是 ,
,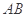 的中点.
的中点.
(Ⅰ)求证: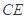 ∥平面
∥平面 ;
;
(Ⅱ)若 到
到 的距离为
的距离为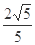 ,求正三棱柱
,求正三棱柱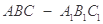 的体积.
的体积.
(本小题满分12分)已知数列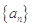 的前
的前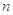 项和
项和 (其中
(其中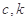 为常数),且
为常数),且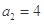 ,
,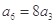 .
.
(Ⅰ)求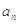 ;
;
(Ⅱ)求数列 的前
的前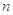 项和
项和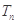 .
.