如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。 .
.
(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
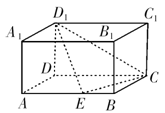
(满分10分)如图4,在长方体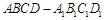 中,
中,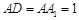 ,
,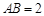 ,点
,点 在棱
在棱 上移动,问
上移动,问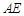 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为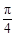 .
.
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DFE∽△EFA;
(2)如果EF=1,求FG的长.
(本小题满分13分)已知数列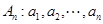 ,
, 满足
满足 ,且当
,且当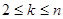 (
(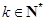 )时,
)时, .令
.令 .
.
(Ⅰ)写出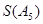 的所有可能取值;
的所有可能取值;
(Ⅱ)求 的最大值.
的最大值.
(本小题满分14分)在平面直角坐标系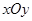 中,点M到两点
中,点M到两点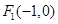 ,
,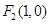 的距离之和为
的距离之和为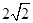 ,设点
,设点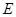 的轨迹为曲线
的轨迹为曲线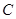 .
.
(Ⅰ)写出曲线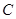 的方程;
的方程;
(Ⅱ)设过点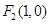 的斜率为
的斜率为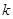 (
(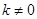 )的直线
)的直线 与曲线
与曲线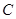 交于不同的两点
交于不同的两点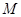 ,
, ,点
,点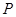 在
在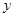 轴上,且
轴上,且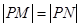 ,求点
,求点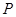 纵坐标的取值范围.
纵坐标的取值范围.
(本小题满分14分)设函数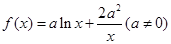 .
.
(Ⅰ)已知曲线 在点
在点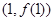 处的切线
处的切线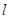 的斜率为
的斜率为 ,求实数
,求实数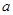 的值;
的值;
(Ⅱ)讨论函数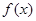 的单调性;
的单调性;
(Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的任意一个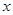 ,都有
,都有 .
.