已知函数 ,m∈R,且
,m∈R,且 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若 +,且
+,且 ,求
,求 的最小值.
的最小值.
(本小题满分10分)选修4—1:几何证明选讲
如图所示, 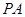 为圆
为圆 的切线,
的切线,  为切点,
为切点,
 ,
,
 的角平分线与
的角平分线与 和圆
和圆 分别交于点
分别交于点 和
和 .
.
(1)求证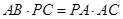
(2)求 的值.
的值.
(本小题满分12分) 已知 (
(
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围.
(本小题满分12分) 设椭圆 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,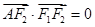 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为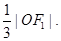
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线 交
交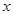 轴于点
轴于点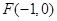 ,交
,交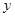 轴于点M,若
轴于点M,若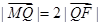 ,求直线
,求直线 的斜率.
的斜率.
(本小题满分12分)如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB= =2,点G为AC的中点.
=2,点G为AC的中点.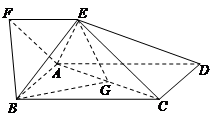
(1)求证:EG//平面ABF;
(2)求三棱锥B-AEG的体积;
(3)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
(本小题满分12分)为调查银川市某校高中生是否愿意提供志愿者服务,用简单随机抽样方法从该校调查了50人,结果如下:
| 是否愿意提供志愿服务 性别 |
愿意 |
不愿意 |
| 男生 |
20 |
5 |
| 女生 |
10 |
15 |
(1)用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人,其中男生抽取多少人?
(2)在(1)中抽取的6人中任选2人,求恰有一名女生的概率;
(3)你能否有99%的把握认为该校高中生是否愿意提供志愿者服务与性别有关?
下面的临界值表供参考:
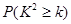 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
独立性检验统计量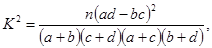 其中
其中