设数列 的前
的前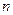 项和为
项和为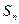 ,且满足
,且满足 ,
, .
.
(Ⅰ)求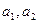 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若正项数列 满足
满足 ,
,
求证:  .
.
(本小题满分12分)如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=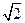 ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.
(Ⅲ)试问:在线段AC上是否存在一点P,使得直线PF与AD所成角为60°?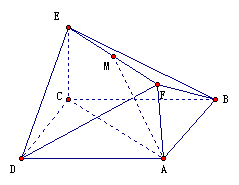
(本小题满分12分)学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数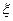 是一个随机变量,求随机变量
是一个随机变量,求随机变量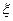 的分布列及数学期望
的分布列及数学期望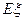 .
.
(本小题满分12分)如图,在棱长为2的正方体 的中点,P为BB1的中点.
的中点,P为BB1的中点.
(I)求证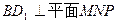 ;
;
(II)求异面直线 所成角的大小;
所成角的大小;
(本小题满分10分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为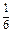 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求三位同学都没有中奖的概率;
(Ⅱ)求三位同学中至少有两位没有中奖的概率.
已知定圆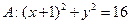 ,动圆
,动圆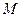 过点
过点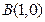 且与圆
且与圆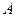 相切,记动圆圆
相切,记动圆圆
心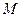 的轨迹为
的轨迹为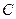 .
.
(Ⅰ)求曲线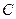 的方程;
的方程;
(Ⅱ)若点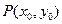 为曲线
为曲线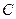 上任意一点,证明直线
上任意一点,证明直线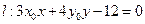 与曲线
与曲线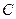 恒有且只有一个公共点.
恒有且只有一个公共点.