在如图所示的几何体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求四面体 的体积;
的体积;
(3)线段 上是否存在点
上是否存在点 ,使
,使 平面
平面 ?请证明你的结论.
?请证明你的结论.
(本小题共13分)设k∈R,函数 ,
, ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性.
(本小题共12分)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
(本小题共12分)
已知函数f(t)= 
 ]
]
(Ⅰ)将函数g(x)化简成Asin(ωx+φ)+B(A>0,ω>0,φ∈[0,2π))的形式;
(Ⅱ)求函数g(x)的值域.
(本小题共12分)已知f(x)=m(x-2m)(x+m+3),g(x)=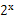 -2,若同时满足条件:
-2,若同时满足条件:
① x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;② x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
(本小题共12分) 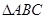 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知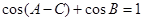 ,
,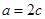 ,求
,求 。
。