(本题满分14分)
如图所示,在正三棱柱ABC -A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点。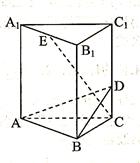
(I)求证:A1B1//平面ABD;
(II)求证:AB⊥CE;
(III)求三棱锥C-ABE的体积。
(本小题满分12分)
已知函数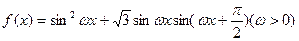 的最小正周期为
的最小正周期为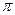 .
.
(Ⅰ)求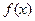 ;
;
(Ⅱ)当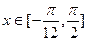 时,求函数
时,求函数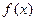 的值域.
的值域.
(本小题满分12分)
如图:在四棱锥 中,底面
中,底面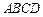 是菱形,
是菱形,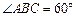 ,
,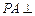 平面
平面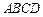 ,
,
点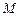 、
、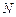 分别为
分别为 、
、 的中点,
的中点,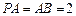 .
.
(I)证明: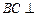 平面
平面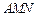 ;
;
(II)在线段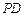 上是否存在一点
上是否存在一点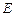 ,使得
,使得 平面
平面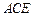 ;若存在,
;若存在, 求出
求出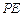 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
函数
(1)求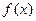 的周期;
的周期;
(2)若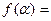
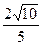 ,
,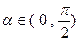 ,求
,求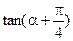 的值
的值
(本题满分14分)已知数列{an}的各项均为正数,观察右上方的程序框图,若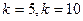 时,分别有
时,分别有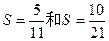
(1)试求数列{an}的通项;
(2)令 ,求数列
,求数列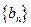 的前
的前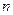 项和
项和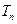 的值.
的值. 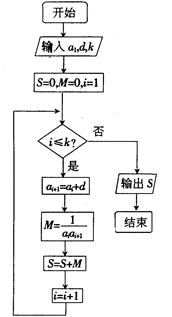
已知实数 ,设P:函数
,设P:函数 在R上单调递减,Q:关于
在R上单调递减,Q:关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,如果命题“
有两个不相等的实数根,如果命题“ ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.