如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 
(1)若直线PQ过定点 ,求点A的坐标;
,求点A的坐标;
(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.
求解下列不等式。
(1)|2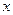 -1|>3(2)
-1|>3(2)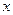 2-5
2-5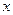 +4≤0
+4≤0
已知函数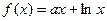 ,
,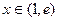 。
。
(Ⅰ)若函数 的图象在x=2处的切线的斜率为1,求实数
的图象在x=2处的切线的斜率为1,求实数 的值;
的值;
(Ⅱ)若 有极值,求实数
有极值,求实数 的取值范围和函数
的取值范围和函数 的值域;
的值域;
(Ⅲ)在(Ⅱ)的条件下,函数 ,证明:
,证明: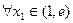 ,
,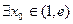 ,使得
,使得 成立
成立
设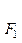 ,
,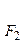 分别是椭圆E:
分别是椭圆E: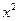 +
+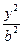 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过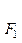 的直线与E相交于A、B两点,且
的直线与E相交于A、B两点,且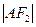 ,
,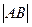 ,
,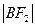 成等差数列。
成等差数列。
(Ⅰ)求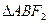 的周长
的周长
(Ⅱ)求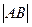 的长
的长
(Ⅲ)若直线的斜率为1,求b的值。
如图,已知三棱锥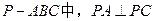 ,
,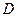 为
为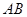 中点,
中点,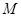 为
为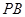 的中点,且
的中点,且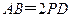 ,.
,.
(I)求证: ;
;
(II)找出三棱锥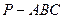 中一组面与面垂直的位置关系,并给出证明(只需找到一组即可)
中一组面与面垂直的位置关系,并给出证明(只需找到一组即可)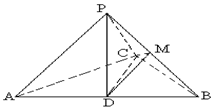
已知函数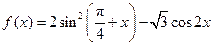 .
.
(Ⅰ)求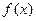 的最小正周期;
的最小正周期;
(Ⅱ)若不等式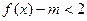 在
在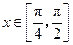 上恒成立,求实数
上恒成立,求实数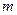 的取值范围.
的取值范围.