已知函数 ,
,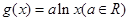 .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为 ,其中
,其中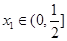 ,求
,求 的最小值.
的最小值.
(本小题满分12分)
设a为实数,函数
(Ⅰ)求f(x)的极值;
(Ⅱ)当 在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
(本小题满分12分)
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为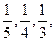 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
(本小题满分12分)
甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加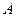 岗位服务的概率;
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率。
(本小题满分10分)
已知函数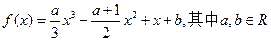 。
。
(Ⅰ)若曲线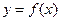 在点
在点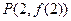 处的切线方程为
处的切线方程为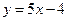 ,求函数
,求函数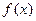 的解析式;
的解析式;
(Ⅱ)当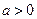 时,讨论函数
时,讨论函数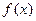 的单调性。
的单调性。
如图,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2M,N分别是A1B1,A1A的中点。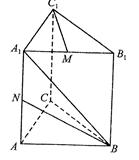
(1)求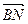 的长度;下
的长度;下
(2)求cos(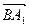 ,
,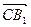 )的值;
)的值;
(3)求证:A1B⊥C1M。