为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.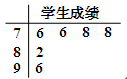
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设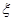 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求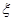 的分布列和期望.
的分布列和期望.
(本小题满分12分)
甲、乙两名射手各进行一次射击,射中环数
 的分布列分别为:
的分布列分别为:
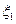 |
8 |
9 |
10 |
| P |
0.3 |
0.5 |
a |
 |
8 |
9 |
10 |
| P |
0.2 |
0.3 |
b |
(I )确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
)确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
(II)两各射手各射击一次为一轮射击,如果在某一轮射击中两人都射中10环,则射击结束,否则继续射击,但最多不超过4轮,求结束时射击轮次数 的分布列及期望,并求结束时射击轮次超过2次的概率。
的分布列及期望,并求结束时射击轮次超过2次的概率。
本小题共12分)
在 中,a,b,c分别为角A,B,C所对的边,向量
中,a,b,c分别为角A,B,C所对的边,向量 且
且
(I)求 的值;
的值;
(II)若b=4, 的面积为
的面积为 的周长。
的周长。
(本小题满分12分)
已知函数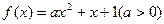 的两个不同的零点为
的两个不同的零点为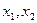
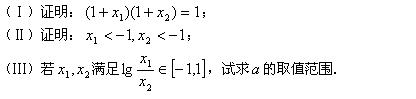
(本小题满分12分)
设关于 的方程
的方程
(Ⅰ)若方程有实数解,求实数 的取值范围;
的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个 数,并求出方程的解.
数,并求出方程的解.
(本小题满分12分)
在平面直角坐标系中, 为坐标原点,
为坐标原点, 三点满足
三点满足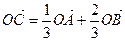
(Ⅰ)求证: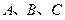 三点共线;
三点共线;
(Ⅱ)求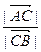 的值;
的值;
(Ⅲ )已知
)已知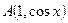 、
、 ,
,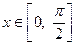
 的最小值为
的最小值为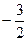 ,求实
,求实 数
数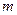 的值.
的值.