学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在一次游戏中,①摸出3个白球的概率,②获奖的概率;
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
(本小题满分14分)已知向量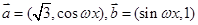 ,函数
,函数
 ·
·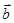 ,
,
且最小正周期为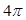 .
.
(1)求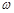 的值;
的值;
(2)设
 ,求
,求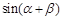 的值.
的值.
(3)若 ,求函数f(x)的值域;
,求函数f(x)的值域;
(本小题满分14分)已知函数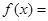
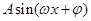 (其中A>0,
(其中A>0, )的图象如图所示.
)的图象如图所示.
(1)求A,w及j的值;
(2)若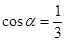 ,求
,求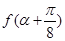 的值.
的值.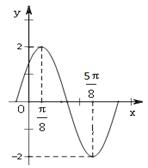
(本小题满分12分)在平面直角坐标系中,点A(-1,-2)、B(2,3)、C(-2,-1).
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足 ,求t的值.
,求t的值.
(本小题满分12分)同时抛三枚质地均匀的硬币
(1)写出所有的基本事件;
(2)求出现“两个正面朝上,一个反面朝上”的概率;
(3)求“至多两个正面朝上”的概率;
(本小题满分14分)已知 是二次函数,不等式
是二次函数,不等式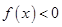 的解集是
的解集是 ,且
,且 在区间
在区间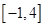 上的最大值是
上的最大值是 .
.
(1)求 的解析式;
的解析式;
(2)设函数 在
在 上的最小值为
上的最小值为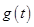 ,求
,求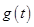 的表达式.
的表达式.