一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
| 加工时间y/分 |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
115 |
122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
(本小题满分13分)如图,在三棱柱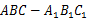 ,
, ⊥平面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
⊥平面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
(1)求证: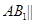 平面
平面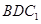 ;
;
(2)若二面角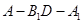 大小为
大小为 ,求直线
,求直线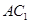 与
与 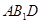 所成角的大小.
所成角的大小.
(本小题满分13分)已知函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若在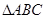 中,角
中,角 ,
,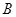 ,
, 的对边分别为
的对边分别为 ,
, ,
,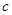 ,
, ,
, 为锐角,且
为锐角,且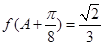 ,求
,求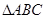 面积
面积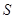 的最大值.
的最大值.
(本小题满分14分)已知a>0,函数 .
.
(1)讨论函数f(x)的单调性;
(2)当函数f(x)存在极值时,设所有极值之和为g(a),求g(a)的取值范围.
(本小题满分12分)椭圆 过点
过点 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点。
两点。
(1)求椭圆 的方程;
的方程;
(2)当 的面积为
的面积为 时,求
时,求 的方程.
的方程.
(本小题满分12分)某学校有男老师45名,女老师15名,按照分层抽样的方法组建了一个4人的学科攻关小组。
(1)求某老师被抽到的概率及学科攻关小组中男、女老师的人数;
(2)经过一个月的学习、讨论,这个学科攻关小组决定选出2名老师做某项实验,方法是先从小组里选出1名老师做实验,该老师做完后,再从小组内剩下的老师中选1名做实验,求选出的2名老师中恰有1名女老师的概率.