为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中，需要志愿者提供帮助的老年人的比例；
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？
(3)根据(2)的结论，能否提出更好的调查方法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由．
附：
| P(K2≥x0) |
0.050 |
0.010 |
0.001 |
| x0 |
3.841 |
6.635 |
10.828 |
χ2＝
（本小题满分10分）. 已知命题p：方程
表示焦点在y轴上的椭圆；
命题q：双曲线
的离心率
；
若“
”为真，“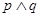
”为假，求实数
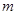的取值范围．
（本小题满分12分）
已知椭圆E的两个焦点分别为F1(－1,0), F2 (1,0), 点(1,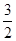 
)在椭圆E上.
(1)求椭圆E的方程
(2)若椭圆E上存在一点 P, 使∠F1PF2=30°, 求△PF1F2的面积.
.(本小题满分12分)
已知直四棱柱ABCD—A′B′C′D′的底面是菱形，
，
E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2.
（1）求证：平面AEF⊥平面AA′C′C；
（2）求截面AEF与底面ABCD的夹角的大小.
（本小题满分14分）
某商店经营的消费品进价每件14元，月销售量Q（百件）与销售价格P（元）的关系如下图，每月各种开支2000元，
（1）写出月销售量Q（百件）与销售价格P（元）的函数关系。
（2）该店为了保证职工最低生活费开支3600元，问：商品价格应控制在什么范围？
（3）当商品价格每件为多少元时，月利润并扣除职工最低生活费的余额最大？并求出最大值。
（本小题满分12分）
直线l经过点
，且和圆C：
相交，截得弦长为
，求l的方程．