A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为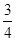 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
己知在锐角三角形中,角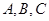 所对的边分别为
所对的边分别为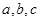 ,且
,且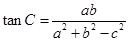
(1)求角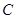 大小;
大小;
(2)当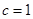 时,求
时,求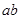 的取值范围
的取值范围
某高校在2014年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官 的面试,设第4组中有
的面试,设第4组中有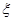 名学生被考官
名学生被考官 面试,求
面试,求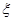 的分布列和数学期望.
的分布列和数学期望.
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有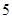 次答题机会,选手累计答对
次答题机会,选手累计答对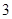 题或答错
题或答错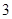 题即终止比赛,答对
题即终止比赛,答对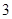 题者直接进入复赛,答错
题者直接进入复赛,答错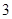 题者则被淘汰.已知选手甲答对每个题的概率均为
题者则被淘汰.已知选手甲答对每个题的概率均为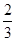 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为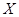 ,试求
,试求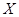 的分布列和数学期望.
的分布列和数学期望.
设直线 的参数方程为
的参数方程为 (
( 为参数,
为参数, 为倾斜角),圆
为倾斜角),圆 的参数方程为
的参数方程为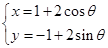 (
( 为参数).
为参数).
(1)若直线 经过圆
经过圆 的圆心,求直线
的圆心,求直线 的斜率.
的斜率.
(2)若直线 与圆
与圆 交于两个不同的点,求直线
交于两个不同的点,求直线 的斜率的取值范围.
的斜率的取值范围.
甲、乙两人各进行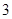 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为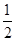 ,乙每次击中目标的概率为
,乙每次击中目标的概率为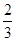 .
.
(1)求乙至多击中目标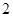 次的概率;
次的概率;
(2)记甲击中目标的次数为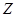 ,求
,求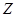 的分布列、数学期望和标准差.
的分布列、数学期望和标准差.