已知点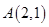 在抛物线
在抛物线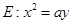 上,直线
上,直线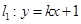 (
(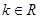 ,且
,且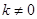 )与抛物线
)与抛物线 ,相交于
,相交于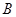 、
、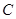 两点,直线
两点,直线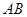 、
、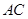 分别交直线
分别交直线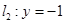 于点
于点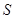 、
、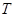 .
.
(1)求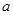 的值;
的值;
(2)若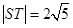 ,求直线
,求直线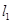 的方程;
的方程;
(3)试判断以线段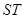 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
在等比数列 中,
中, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,且
,且 为递增数列,若
为递增数列,若 ,求证:
,求证: .
.
在 中,内角
中,内角 所对边分别为
所对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 面积的最大值.
面积的最大值.
已知命题 “存在
“存在 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”.
表示双曲线”.
(1)若“ 且
且 ”是真命题,求
”是真命题,求 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
已知函数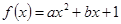 (
(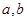 为实数),
为实数),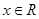 ,
,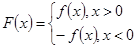 .
.
(1)若 ,且函数
,且函数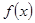 的值域为
的值域为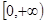 ,求
,求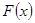 的表达式;
的表达式;
(2)在(1)的条件下,当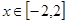 时,
时,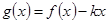 是单调函数,求实数
是单调函数,求实数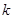 的取值范围;
的取值范围;
(3)设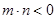 ,
,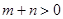 ,
,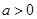 且
且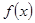 为偶函数,判断
为偶函数,判断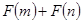 能否大于零.
能否大于零.
如图:A、B两城相距100 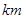 ,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气.已知D地距A城
,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气.已知D地距A城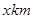 ,为保证城市安全,天燃气站距两城市的距离均不得少于10
,为保证城市安全,天燃气站距两城市的距离均不得少于10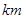 .已知建设费用
.已知建设费用 (万元)与A、B两地的供气距离(
(万元)与A、B两地的供气距离(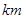 )的平方和成正比,当天燃气站D距A城的距离为40
)的平方和成正比,当天燃气站D距A城的距离为40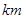 时, 建费用为1300万元.(供气距离指天燃气站距到城市的距离)
时, 建费用为1300万元.(供气距离指天燃气站距到城市的距离)
(1)把建设费用 (万元)表示成供气距离
(万元)表示成供气距离 (
(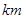 )的函数,并求定义域;
)的函数,并求定义域;
(2)天燃气供气站建在距A城多远,才能使建设供气费用最小,最小费用是多少?