在 中,内角
中,内角 所对边分别为
所对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 面积的最大值.
面积的最大值.
某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数: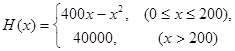 ,其中
,其中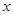 是仪器的月产量(总收入=总成本+利润).
是仪器的月产量(总收入=总成本+利润).
(Ⅰ)将利润(用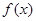 表示)表示为月产量
表示)表示为月产量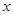 的函数;
的函数;
(Ⅱ)当月产量为何值时,车间所获利润最大?最大利润是多少元?
已知函数 在
在 上有最大值1和最小值0,设
上有最大值1和最小值0,设 (
(
为自然对数的底数).
(1)求 的值;
的值;
(2)若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
已知数列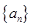 中,
中,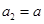 (
( 为非零常数),其前n项和
为非零常数),其前n项和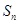 满足
满足 .
.
(1)求数列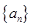 的通项公式;
的通项公式;
(2)若 ,且
,且 ,求
,求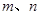 的值;
的值;
(3)是否存在实数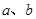 ,使得对任意正整数
,使得对任意正整数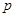 ,数列
,数列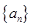 中满足
中满足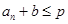 的最大项恰为第
的最大项恰为第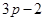 项?
项?
若存在,分别求出 与
与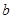 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
如图,已知海岛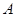 到海岸公路
到海岸公路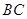 的距离
的距离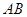 为50km,
为50km,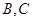 间的距离为100km,从
间的距离为100km,从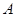 到
到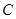 ,
,
必须先坐船到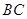 上的某一点
上的某一点 ,船速为
,船速为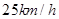 ,再乘汽车到
,再乘汽车到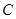 ,车速为
,车速为 ,记
,记 .
.
(1)试将由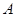 到
到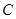 所用的时间
所用的时间 表示为
表示为 的函数
的函数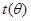 ;
;
(2)问 为多少时,由
为多少时,由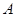 到
到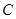 所用的时间
所用的时间 最少?
最少?
如图,已知椭圆 的右顶点为
的右顶点为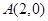 ,点
,点 在椭圆上(
在椭圆上(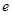 为椭圆
为椭圆
的离心率).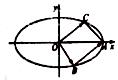
(1)求椭圆的方程;
(2)若直线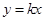 和椭圆交于点
和椭圆交于点 (
( 在第一象限内),且点
在第一象限内),且点 也在椭圆上,
也在椭圆上,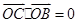 ,若
,若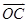 与
与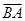
共线,求实数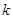 的值 .
的值 .