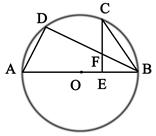
如图: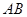 是⊙
是⊙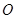 的直径,
的直径,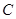 是弧
是弧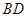 的中点,
的中点, ⊥
⊥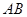 ,垂足为
,垂足为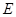 ,
,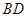 交
交 于点
于点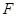 .
.
(1)求证: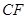 =
=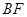 ;
;
(2)若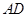 =4,⊙
=4,⊙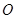 的半径为6,求
的半径为6,求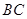 的长.
的长.
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: .

(1)求图中
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(
)与数学成绩相应分数段的人数(
)之比如下表所示,求数学成绩在
之外的人数.
分数段

已知函数
,
,且
.
(1)求
的值;
(2)设
,
,
,求
的值.
设函数
,其中
。
(1)当
时,求不等式
的解集;
(2)若不等式
的解集为
,求
的值。
在直角坐标系
中,曲线
的参数方程为
,
是
上的动点,
点满足 ,
点的轨迹为曲线
.
,
点的轨迹为曲线
.
(1)求
的方程
(2)在以
为极点,
轴的正半轴为极轴的极坐标系中,射线
与
的异于极点的交点为
,与
的异于极点的交点为
,求
.
如图, 分别为 的边 上的点,且不与 的顶点重合。已知 的长为 , 的长为 , 的长是关于 的方程 的两个根。

(1)证明:
四点共圆;
(2)若
,且
,求
所在圆的半径。