如图,从A1(1,0,0)、A2(2,0,0)、B1(0,1,0)、B2(0,2,0)、C1(0,0,1)、C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).
(1)求V=0的概率;
(2)求V的分布列及数学期望E(V).
已知函数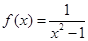 .
.
(1)设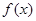 的定义域为A,求集合A;
的定义域为A,求集合A;
(2)判断函数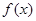 在(1,+
在(1,+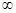 )上单调性,并用定义加以证明.
)上单调性,并用定义加以证明.
计算:
(1)集合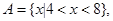 集合
集合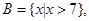 求
求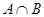 和
和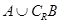
(2)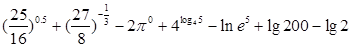
已知数列 的前
的前 项和为
项和为 ,且
,且 。
。
(1)求数列 的通项公式与前
的通项公式与前 项的和
项的和 ;
;
(2)设 ,若集合
,若集合 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围。
的取值范围。
某校高中三个年级共有学生1800名,各年级男生、女生的人数如下表:
| 高一年级 |
高二年级 |
高三年级 |
|
| 男生 |
290 |
b |
344 |
| 女生 |
260 |
c |
 |
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为0.17.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知 ,求高二年级男生比女生多的概率。
,求高二年级男生比女生多的概率。
在 中,内角
中,内角 所对边长分别为
所对边长分别为 ,已知
,已知
且 。
。
(1)求角 的值;
的值;
(2)若 ,求
,求 的值。
的值。