矩阵M= 有特征向量为e1=
有特征向量为e1= ,e2=
,e2= ,
,
(1)求e1和e2对应的特征值;
(2)对向量α= ,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.
,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.
已知函数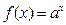 (
( ,
,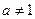 )在
)在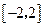 上函数值总小于
上函数值总小于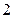 ,求实数
,求实数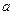 的取值范围.
的取值范围.
求函数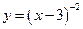 的定义域,并指出函数的单调区间.
的定义域,并指出函数的单调区间.
如果我国的GDP年平均增长率保持为 ,约多少年后我国的GDP在1999年的基础上翻两番?
,约多少年后我国的GDP在1999年的基础上翻两番?
已知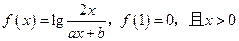 时,恒有
时,恒有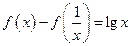 .
.
(1)求常数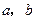 的值;(2)求
的值;(2)求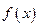 的定义域.
的定义域.
每一行星都按照一个椭圆轨道绕太阳运行.行星的轨道周期 是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的
是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的 次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为
次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为 亿千米,地球的运行周期是多少(以年计)?
亿千米,地球的运行周期是多少(以年计)?