已知正数a、b、c满足abc=1,求证:(a+2)(b+2)(c+2)≥27.
(本小题满分12分)设函数 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若 ,且点P的横坐标为
,且点P的横坐标为 .
.
(1),求证:P点的纵坐标为定值,并求出这个定值;
(2),求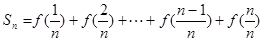
(3),记Tn为数列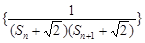 的前n项和,若
的前n项和,若 对一切n∈N*都成立,试求a的取值范围。
对一切n∈N*都成立,试求a的取值范围。
(本小题满分10分)求过点P(2,2)且与曲线y=x2相切的直线方程.
已知数列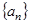 的前
的前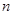 项和
项和 满足
满足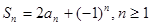 .
.
(1)写出数列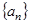 的前三项
的前三项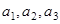 ;
;
(2)求数列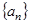 的通项公式;
的通项公式;
(3)证明:对任意的整数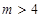 ,有
,有 .
.
在 中,
中, 的对边分别为
的对边分别为 且
且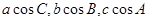 成等差数列.
成等差数列.
(1)求B的值;
(2)求 的范围.
的范围.
已知数列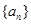 的前n项和为
的前n项和为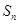 ,且
,且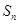
 ,
,
(1)求数列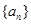 的通项公式;
的通项公式;
(2) 令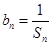 ,且数列
,且数列 的前n项和为
的前n项和为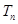 ,求
,求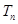 ;
;
(3)若数列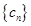 满足条件:
满足条件: ,又
,又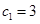 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列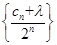 为等差数列?
为等差数列?