本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分6分
已知函数 .
.
⑴若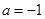 ,解方程
,解方程 ;
;
⑵若函数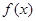 在
在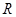 上单调递增,求实数
上单调递增,求实数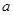 的取值范围;
的取值范围;
⑶是否存在实数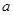 ,使不等式
,使不等式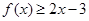 对一切实数
对一切实数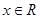 恒成立?若存在,求出
恒成立?若存在,求出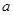 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分12分)
已知椭圆M的中心为坐标原点,且焦点在x轴上,若M的一个顶点恰好是抛物线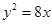 的焦点,M的离心率
的焦点,M的离心率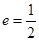 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线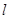 ,交M于A,B两点.
,交M于A,B两点.
(1)求椭圆M的标准方程;
(2)设点N(t,0)是一个动点,且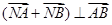 ,求实数t的取值范围.
,求实数t的取值范围.
(本小题满分12分)
哈尔滨冰雪大世界每年冬天都会吸引大批游客,现准备在景区内开设经营热饮等食品的店铺若干.根据以往对500名40岁以下(含40岁)人员和500名40岁以上人员的统计调查,有如下一系列数据:40岁以下(含40岁)人员购买热饮等食品的有260人,不购买热饮食品的有240人;40岁以上人员购买热饮等食品的有220人,不购买热饮等食品的有280人,请根据以上数据作出2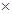 2列联表,并运用独立性检验思想,判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系?
2列联表,并运用独立性检验思想,判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系?
注:要求达到99. 9%的把握才能认定为有关系.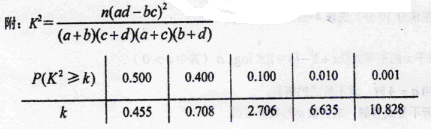 s
s
(本小题满分12分)
已知斜三棱柱ABC—A1B1C1的底面是正三角形,侧面ABB1A1是边长为2的菱形,且 ,M是AB的中点,
,M是AB的中点,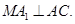
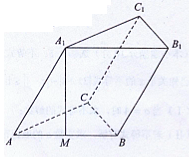
(1)求证: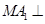 平面ABC;
平面ABC;
(2)求点M到平面AA1C1C的距离.
(本小题满分12分)
已知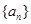 为等比数列,
为等比数列, 为等差数列
为等差数列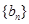 的前n项和,
的前n项和,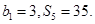
(1)求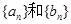 的通项公式;
的通项公式;
(2)设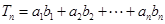 ,求
,求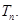
设函数 ,其中
,其中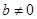 。
。
⑴当 时,判断函数
时,判断函数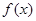 在定义域上的单调性;
在定义域上的单调性;
⑵求函数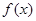 的极值点;
的极值点;
⑶证明对任意的正整数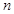 ,不等式
,不等式 成立。
成立。