已知 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前n项和
的前n项和 .
.
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
| 所用时间(min) |
10~20 |
20~30 |
30~40 |
40~50 |
50~60 |
| 选择L1人数 |
6 |
12 |
18 |
12 |
12 |
| 选择L2人数 |
0 |
4 |
16 |
16 |
4 |
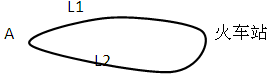
(1)试估计40 min内不能赶到火车站的概率
(2)现甲有40 min时间赶往火车站,为尽最大可能在允许的时间内赶到火车站,试通过计算说明,他如何选路径
将一个质地均匀的正方形骰子先后抛掷两次,计算其中向上的数之和是5的结果有多少种;求向上的数之和是5的概率;求向上的数之和是3的倍数的概率。
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
[230,235) |
8 |
0.16 |
| 第二组 |
[235,240) |
① |
0.24 |
| 第三组 |
[240,245) |
15 |
② |
| 第四组 |
[245,250) |
10 |
0.20 |
| 第五组 |
[250,255] |
5 |
0.10 |
| 合计 |
50 |
1.00 |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
欲修建一横断面为等腰梯形(如图1)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?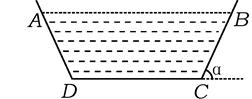
分析方程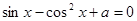 在
在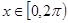 的解的个数.
的解的个数.