古希腊著名的毕达哥拉斯学派把1、3、6、10 …，这样的数称为“三角形数”，而把1、4、9、16…，这样的数称为“正方形数”．
（1）第5个三角形数是 ，第n个“三角形数”是 ，第5个“正方形数”是 ，第n个正方形数是 ；
（2）经探究我们发现：任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．
例如：①4=1+3，②9=3+6，③16=6+10，④ ，⑤ ，…．
请写出上面第4个和第5个等式；
（3）在（2）中，请探究第n个等式，并证明你的结论．
某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了两种优惠办法。
A种办法:卖一支毛笔就赠送一本书法练习本；
B种办法:按购买金额打九折付款。
某校欲为校书法兴趣小组购买这种毛笔10支,书法练习本x(x
)本。
（1）写出每本优惠办法实际付款金额y(元)与x(本)之间的函数关系式；
（2）比较购买同样多的书法练习本时,按那种优惠办法付款更省钱。
如图，已知点A（－6，0），点B和C在y轴正半轴上，∠CAO＝60°，若点B到直线AC的距离是
，求直线AC的解析式和点B的坐标。
从甲、乙两种饮料中各抽取10盒250毫升的果汁饮料，检查其中的维生素C的含量，所得数据如下（单位：毫克）：
甲：120、123、119、121、122、124、119、122、121、119
乙：121、119、124、119、123、124、123、122、123、122
通过计算说明哪种饮料维生素C的含量高？哪种饮料维生素C的含量比较稳定？
某水库的拦水大坝的横截面是个梯形，AD//BC，如图所示。已知斜坡AB的坡度为i =1∶1 ，∠ADC=150º，又AD=20米，AB=28米。求BC的长度。（参考数据：
、
，
）
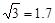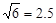如图，在△ABC中，AB＝8, AC＝6, 点D在AC上，AD＝2，试在AB上画出点E，使得△ADE和△ABC相似，并求出AE的长。