如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是 棱AP,AC,BC,PB的中点.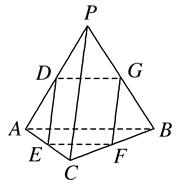
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
如图, 在直三棱柱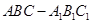 中,
中,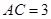 ,
,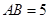 ,
,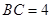
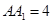 ,点
,点 是
是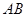 的中点.
的中点.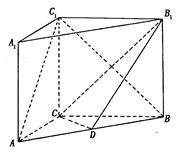
⑴求证: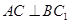 ;
;
⑵求证: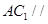 平面
平面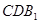 ;
;
⑶求二面角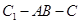 的正切值.
的正切值.
甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队中每人答对的概率均为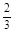 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为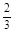 ,
,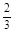 ,
,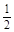 ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用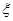 表示甲队的总得分.
表示甲队的总得分.
(1)求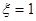 的概率及
的概率及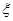 的数学期望
的数学期望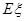 ;
;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求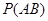 .
.
已知:△ABC中角A、B、C所对的边分别为
且 .
.
(1)求角C的大小;
(2)若 成等差数列,且
成等差数列,且 ,求边
,求边 的长.
的长.
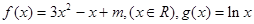
(1)若函数 f(x)与 g(x)的图像在 x=x0处的切线平行,求x0的值
(2)当曲线 有公共切线时,求函数
有公共切线时,求函数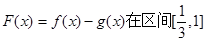 上的最值
上的最值
(3)求证:当m>-2时,对一切正整数n,不等式f(x)> g(x)在区间 [n,n+1]上恒成立
若椭圆C: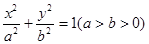 上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2
上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2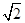 ,△PF1F2s的面积最大值为1
,△PF1F2s的面积最大值为1
(I)求椭圆的方程
(II)若过点M(2,0)的直线l与椭圆C交于不同两点A、B,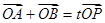 (O为坐标原点)且
(O为坐标原点)且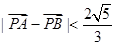 | ,求实数t的取值范围.
| ,求实数t的取值范围.