如图，平面 PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O分别为 PA，PB，AC的中点，AC＝16，PA＝PC＝10. 
(1)设G是OC的中点，证明：FG∥平面BOE；
(2)证明：在△ABO内存在一点M，使FM⊥平面BOE.
（本小题满分12分）一厂家向用户提供的一箱产品共10件，其中有2件次品，
用户先对产品进行抽检以决定是否接收．抽检规则是：一次取一件产品检查（取出的产品不
放回箱子），若前三次没有抽查到次品，则用户接收这箱产品；若前三次中一旦抽查到次品
就立即停止抽检，并且用户拒绝接收这箱产品．
（1）求这箱产品被用户接收的概率；
（2）记抽检的产品件数为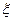
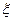，求的分布列和数期望．
（本小题满分10分）解关于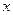
的不等式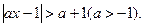
（本小题满分12分）已知函数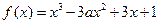
．
（1）设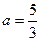
，求函数
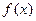在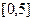
上的最大值和最小值；
（2）设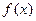在区间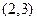
中至少有一个极值点，求
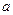的取值范围．
（本小题满分12分）已知函数
，曲线
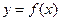在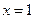
处的切线为l：
．
（1）若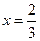
时，函数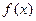
有极值，求函数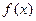的解析式；
（2）若函数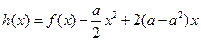
，求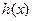
的单调递增区间（其中
）．
（本小题满分12分）
已知函数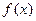
=
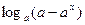（a＞1）．
（1）求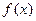的定义域、值域，并判断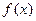的单调性；
（2）解不等式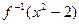
＞．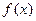